Summary

We need to find the rectangle of largest area that can be formed by using the given bars of histogram.

Solution

Approach #1 Brute Force [Time Limit Exceeded]

Firstly, we need to take into account the fact that the height of the rectangle\nformed between any two bars will always be limited by the height of the shortest\nbar lying between them which can be understood by looking at the figure below:

Thus, we can simply start off by considering every possible\npair of bars and finding the area of the rectangle formed between them using the\nheight of the shortest bar lying between them as the height\n and the spacing between\nthem as the width of the rectangle. We can thus, find the required rectangle with the\n maximum area.

Complexity Analysis

\n
• Time complexity : $$O(n^3)$$ . We have to find the minimum height bar $$\\big(O(n)\\big)$$ lying\nbetween every pair $$\\big(O(n^2)\\big)$$ .
\n
• Space complexity : $$O(1)$$ . Constant space is used.
\n

Approach #2 Better Brute Force[Time Limit Exceeded]

Algorithm

We can do one slight modification in the previous approach to optimize it to some extent.\n Instead of taking every possible pair and then finding the bar of minimum height\n lying between them everytime, we can find the bar of minimum height for\n current pair by using the minimum height bar of the previous pair.

In mathematical terms, $$minheight=\\min(minheight, heights(j))$$ , where $$heights(j)$$ \n refers to the height of the $$j$$ th bar.

Complexity Analysis

\n
• \n

  Time complexity : $$O(n^2)$$ . Every possible pair is considered

  \n
\n
• \n

  Space complexity : $$O(1)$$ . No extra space is used.

  \n
\n

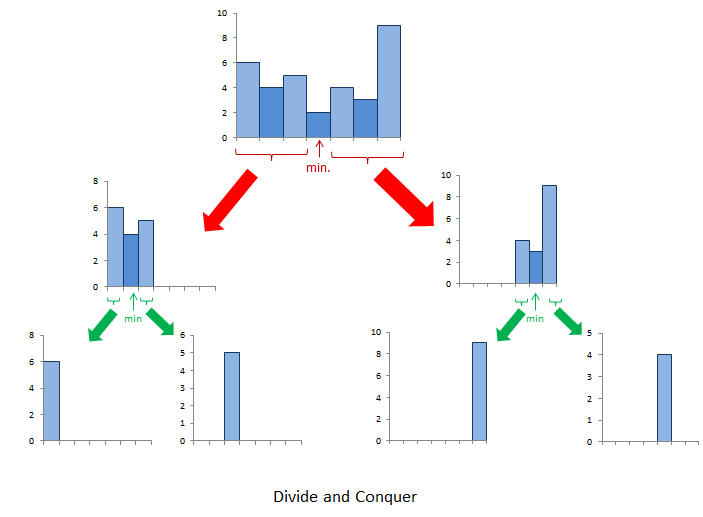
Approach #3 (Divide and Conquer Approach) [Time Limit Exceeded]

Algorithm

This approach relies on the observation that the rectangle with maximum area will be\nthe maximum of:

\n
1. \n

   The widest possible rectangle with height equal to the height of the shortest bar.

   \n
\n
2. \n

   The largest rectangle confined to the left of the shortest bar(subproblem).

   \n
\n
3. \n

   The largest rectangle confined to the right of the shortest bar(subproblem).

   \n
\n

Let\'s take an example:

[6, 4, 5, 2, 4, 3, 9]\n

Here, the shortest bar is of height 2. The area of the widest rectangle using this\n bar as height is 2x8=16. Now, we need to look for cases 2 and 3 mentioned above.\n Thus, we repeat the same process to the left and right of 2. In the left of 2, 4\n is the minimum, forming an area of rectangle 4x3=12. Further, rectangles of area 6x1=6 and\n 5x1=5 exist in its left and right respectively. Similarly we find an area of 3x3=9, 4x1=4 and 9x1=9\n to the left of 2. Thus, we get 16 as the correct maximum area. See the figure below for further clarification:

Complexity Analysis

\n
• \n

  Time complexity :

  \n

  Average Case: $$O\\big(n \\log(n)\\big)$$ .

  \n

  Worst Case: $$O(n^2)$$ . If the numbers in the array are sorted,\n we don\'t gain the advantage of divide and conquer.

  \n
\n
• \n

  Space complexity : $$O(n)$$ . Recursion with worst case depth $$n$$ .

  \n
\n

Approach #4 (Better Divide and Conquer) [Accepted]

Algorithm

You can observe that in the Divide and Conquer Approach, we gain the advantage, since\n the large problem is divided into substantially smaller subproblems. But, we won\'t gain\n much advantage with that approach if the array happens to be sorted in either\n ascending or descending order, since every time we need to find the minimum number in a\n large subarray $$\\big(O(n)\\big)$$ . Thus, the overall complexity becomes $$O(n^2)$$ in the worst case.\n We can reduce the time complexity by using a Segment Tree to find the minimum every time which\n can be done in $$O\\big(\\log(n)\\big)$$ time.

For implementation, click here.

Complexity Analysis

\n
• \n

  Time complexity : $$O\\big(n\\log(n)\\big)$$ . Segment tree takes $$log(n)$$ \n $$n$$ times.

  \n
\n
• \n

  Space complexity : $$O(n)$$ . Space required for Segment Tree.

  \n
\n

Approach #5 (Using Stack) [Accepted]

Algorithm

In this approach, we maintain a stack. Initially, we push a -1 onto the stack to mark the end.\nWe start with the leftmost bar and keep\npushing the current bar\'s index onto the stack until we get two successive numbers\n in descending order, i.e. until we get $$a[i]<a[i-1]$$ . Now, we start popping the\n numbers from the stack until we hit a number $$stack[j]$$ on the stack such that $$a\\big[stack[j]\\big] \\leq a[i]$$ .\n Every time we pop, we find out the area of rectangle formed using the current element as the height\n of the rectangle and the difference between the the current element\'s index pointed to in the original array and the element $$stack[top-1] -1$$ as the width\n i.e. if we pop an element $$stack[top]$$ and i is the current index to which we are pointing in the original array, the current area of the rectangle will be considered as $$(i-stack[top-1]-1) \\times a\\big[stack[top]\\big]$$ .

Further, if we reach the end of the array, we pop all the elements of the\n stack and at every pop, this time we use the following equation to find the area:\n $$(stack[top]-stack[top-1]) \\times a\\big[stack[top]\\big]$$ , where $$stack[top]$$ refers to the\n element just popped. Thus, we can get the area of the\n of the largest rectangle by comparing the new area found everytime.

The following example will clarify the process further:\n [6, 7, 5, 2, 4, 5, 9, 3]

!?!../Documents/84_Largest_Rectangle.json:1000,563!?!

Complexity Analysis

\n
• \n

  Time complexity : $$O(n)$$ . $$n$$ numbers are pushed and popped.

  \n
\n
• \n

  Space complexity : $$O(n)$$ . Stack is used.

  \n
\n

Analysis written by: @vinod23