Approach #1 Hash Table [Accepted]

Intuition

If we keep track of the nodes that we\'ve seen already in a Set, we can\ntraverse the list and return the first duplicate node.

Algorithm

First, we allocate a Set to store ListNode references. Then, we traverse\nthe list, checking visited for containment of the current node. If the node\nhas already been seen, then it is necessarily the entrance to the cycle. If\nany other node were the entrance to the cycle, then we would have already\nreturned that node instead. Otherwise, the if condition will never be\nsatisfied, and our function will return null.

The algorithm necessarily terminates for any list with a finite number of\nnodes, as the domain of input lists can be divided into two categories:\ncyclic and acyclic lists. An acyclic list resembles a null-terminated chain\nof nodes, while a cyclic list can be thought of as an acyclic list with the\nfinal null replaced by a reference to some previous node. If the while\nloop terminates, we return null, as we have traversed the entire list\nwithout encountering a duplicate reference. In this case, the list is\nacyclic. For a cyclic list, the while loop will never terminate, but at\nsome point the if condition will be satisfied and cause the function to\nreturn.

Complexity Analysis

\n
• Time complexity : $$O(n)$$ \n
\n

For both cyclic and acyclic inputs, the algorithm must visit each node\nexactly once. This is transparently obvious for acyclic lists because the\n $$n$$ th node points to null, causing the loop to terminate. For cyclic\nlists, the if condition will cause the function to return after\nvisiting the $$n$$ th node, as it points to some node that is already in\nvisited. In both cases, the number of nodes visited is exactly $$n$$ ,\nso the runtime is linear in the number of nodes.

\n
• Space complexity : $$O(n)$$ \n
\n

For both cyclic and acyclic inputs, we will need to insert each node into\nthe Set once. The only difference between the two cases is whether we\ndiscover that the "last" node points to null or a previously-visited\nnode. Therefore, because the Set will contain $$n$$ distinct nodes, the\nmemory footprint is linear in the number of nodes.

Approach #2 Floyd\'s Tortoise and Hare [Accepted]

Intuition

What happens when a fast runner (a hare) races a slow runner (a tortoise) on\na circular track? At some point, the fast runner will catch up to the slow\nrunner from behind.

Algorithm

Floyd\'s algorithm is separated into two distinct phases. In the first\nphase, it determines whether a cycle is present in the list. If no cycle is\npresent, it returns null immediately, as it is impossible to find the\nentrance to a nonexistant cycle. Otherwise, it uses the located "intersection\nnode" to find the entrance to the cycle.

Phase 1

Here, we initialize two pointers - the fast hare and the slow tortoise.\nThen, until hare can no longer advance, we increment tortoise once and\nhare twice.¹ If, after advancing them, hare and tortoise point to\nthe same node, we return it. Otherwise, we continue. If the while loop\nterminates without returning a node, then the list is acyclic, and we return\nnull to indicate as much.

To see why this works, consider the image below:

\n\n

Here, the nodes in the cycle have been labelled from 0 to $$C-1$$ , where\n $$C$$ is the length of the cycle. The noncyclic nodes have been labelled from\n $$-F$$ to -1, where $$F$$ is the number of nodes outside of the cycle. After\n $$F$$ iterations, tortoise points to node 0 and hare points to some node\n $$h$$ , where $$F \\equiv h \\pmod C$$ . This is because hare traverses $$2F$$ \nnodes over the course of $$F$$ iterations, exactly $$F$$ of which are in the\ncycle. After $$C-h$$ more iterations, tortoise obviously points to node\n $$C-h$$ , but (less obviously) hare also points to the same node. To see why,\nremember that hare traverses $$2(C-h)$$ from its starting position of $$h$$ :

\n $$\n\\begin{aligned}\n h + 2(C-h) &= 2C - h \\\\ \n &\\equiv C-h \\pmod C\n\\end{aligned}\n$$ \n

Therefore, given that the list is cyclic, hare and tortoise will\neventually both point to the same node, known henceforce as the\nintersection.

Phase 2

Given that phase 1 finds an intersection, phase 2 proceeds to find the node\nthat is the entrance to the cycle. To do so, we initialize two more pointers:\nptr1, which points to the head of the list, and ptr2, which points to\nthe intersection. Then, we advance each of them by 1 until they meet; the\nnode where they meet is the entrance to the cycle, so we return it.

Use the diagram below to help understand the proof of this approach\'s\ncorrectness.

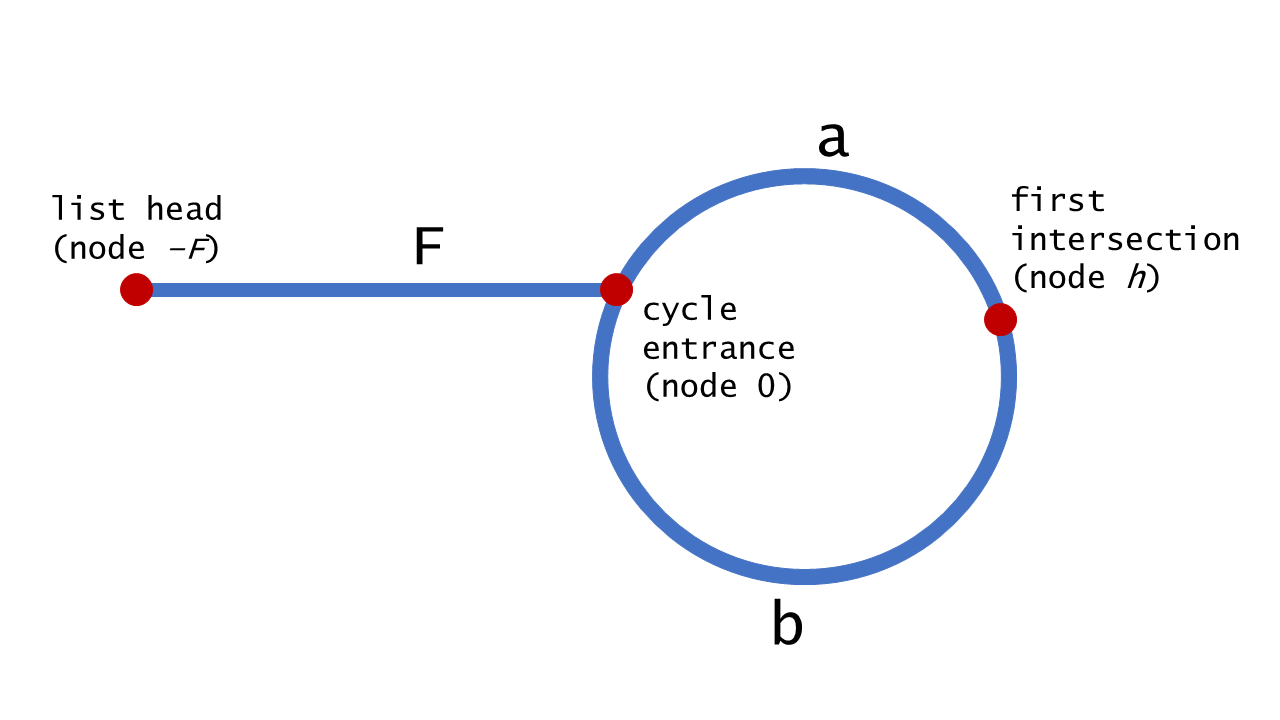\n\n

We can harness the fact that hare moves twice as quickly as tortoise to\nassert that when hare and tortoise meet at node $$h$$ , hare has\ntraversed twice as many nodes. Using this fact, we deduce the following:

\n $$\n\\begin{aligned}\n 2 \\cdot distance(tortoise) &= distance(hare) \\\\\n 2(F+a) &= F+a+b+a \\\\\n 2F+2a &= F+2a+b \\\\\n F &= b \\\\\n\\end{aligned}\n$$ \n

Because $$F=b$$ , pointers starting at nodes $$h$$ and $$0$$ will traverse the\nsame number of nodes before meeting.

To see the entire algorithm in action, check out the animation below:

!?!../Documents/142_Linked_List_Cycle_II.json:1280,720!?!

Complexity Analysis

\n
• \n

  Time complexity : $$O(n)$$ \n

  \n

  For cyclic lists, hare and tortoise will point to the same node after\n $$F+C-h$$ iterations, as demonstrated in the proof of correctness.\n $$F+C-h \\leq F+C = n$$ , so phase 1 runs in $$O(n)$$ time. Phase 2\nruns for $$F < n$$ iterations, so it also runs in $$O(n)$$ time.

  \n

  For acyclic lists, hare will reach the end of the list in roughly\n $$\\frac{n}{2}$$ iterations, causing the function to return before phase\n2. Therefore, regardless of which category of list the algorithm\nreceives, it runs in time linearly proportional to the number of nodes.

  \n
\n
• \n

  Space complexity : $$O(1)$$ \n

  \n

  Floyd\'s Tortoise and Hare algorithm allocates only pointers, so it runs\nwith constant overall memory usage.

  \n
\n

Footnotes

Analysis and solutions written by: @emptyset

Proof of phase 1 inspired by paw88789\'s answer here.

Proof of phase 2 inspired by Old Monk\'s answer here.