Approach #1 Brute Force [Time Limit Exceeded]

Intuition

Because a sequence could start at any number in nums, we can exhaust the\nentire search space by building as long a sequence as possible from every\nnumber.

Algorithm

The brute force algorithm does not do anything clever - it just considers\neach number in nums, attempting to count as high as possible from that\nnumber using only numbers in nums. After it counts too high (i.e.\ncurrentNum refers to a number that nums does not contain), it records the\nlength of the sequence if it is larger than the current best. The algorithm\nis necessarily optimal because it explores every possibility.

Complexity Analysis

\n
• \n

  Time complexity : $$O(n^3)$$ .

  \n

  The outer loop runs exactly $$n$$ times, and because currentNum\nincrements by 1 during each iteration of the while loop, it runs in\n $$O(n)$$ time. Then, on each iteration of the while loop, an $$O(n)$$ \nlookup in the array is performed. Therefore, this brute force algorithm\nis really three nested $$O(n)$$ loops, which compound multiplicatively to a\ncubic runtime.

  \n
\n
• \n

  Space complexity : $$O(1)$$ .

  \n

  The brute force algorithm only allocates a handful of integers, so it uses constant\nadditional space.

  \n
\n

Approach #2 Sorting [Accepted]

Intuition

If we can iterate over the numbers in ascending order, then it will be\neasy to find sequences of consecutive numbers. To do so, we can sort the\narray.

Algorithm

Before we do anything, we check for the base case input of the empty array.\nThe longest sequence in an empty array is, of course, 0, so we can simply\nreturn that. For all other cases, we sort nums and consider each number\nafter the first (because we need to compare each number to its previous\nnumber). If the current number and the previous are equal, then our current\nsequence is neither extended nor broken, so we simply move on to the next\nnumber. If they are unequal, then we must check whether the current number\nextends the sequence (i.e. nums[i] == nums[i-1] + 1). If it does, then we\nadd to our current count and continue. Otherwise, the sequence is broken, so\nwe record our current sequence and reset it to 1 (to include the number that\nbroke the sequence). It is possible that the last element of nums is part\nof the longest sequence, so we return the maximum of the current sequence and\nthe longest one.

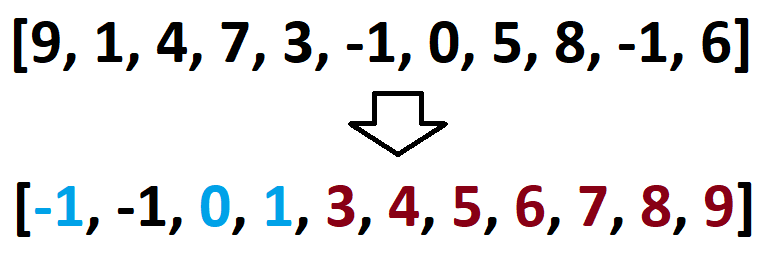
Here, an example array is sorted before the linear scan identifies all consecutive sequences.\nThe longest sequence is colored in red.

Complexity Analysis

\n
• \n

  Time complexity : $$O(nlgn)$$ .

  \n

  The main for loop does constant work $$n$$ times, so the algorithm\'s time\ncomplexity is dominated by the invocation of sort, which will run in\n $$O(nlgn)$$ time for any sensible implementation.

  \n
\n
• \n

  Space complexity : $$O(1)$$ (or $$O(n)$$ ).

  \n

  For the implementations provided here, the space complexity is constant\nbecause we sort the input array in place. If we are not allowed to modify\nthe input array, we must spend linear space to store a sorted copy.

  \n
\n

Approach #3 HashSet and Intelligent Sequence Building [Accepted]

Intuition

It turns out that our initial brute force solution was on the right track, but missing\na few optimizations necessary to reach $$O(n)$$ time complexity.

Algorithm

This optimized algorithm contains only two changes from the brute force\napproach: the numbers are stored in a HashSet (or Set, in Python) to\nallow $$O(1)$$ lookups, and we only attempt to build sequences from numbers\nthat are not already part of a longer sequence. This is accomplished by first\nensuring that the number that would immediately precede the current number in\na sequence is not present, as that number would necessarily be part of a\nlonger sequence.

Complexity Analysis

\n
• \n

  Time complexity : $$O(n)$$ .

  \n

  Although the time complexity appears to be quadratic due to the while\nloop nested within the for loop, closer inspection reveals it to be\nlinear. Because the while loop is reached only when currentNum marks\nthe beginning of a sequence (i.e. currentNum-1 is not present in\nnums), the while loop can only run for $$n$$ iterations throughout the\nentire runtime of the algorithm. This means that despite looking like\n $$O(n*n)$$ complexity, the nested loops actually run in $$O(n + n) = O(n)$$ \ntime. All other computations occur in constant time, so the overall\nruntime is linear.

  \n
\n
• \n

  Space complexity : $$O(n)$$ .

  \n

  In order to set up $$O(1)$$ containment lookups, we allocate linear space\nfor a hash table to store the $$O(n)$$ numbers in nums. Other than that,\nthe space complexity is identical to that of the brute force solution.

  \n
\n

Analysis written by: @emptyset