\n\n

Approach #1 Brute Force [Time Limit Exceeded]

\n

Intuition

\n

We can exhaust the search space in quadratic time by checking whether each\nelement is the majority element.

\n

Algorithm

\n

The brute force algorithm iterates over the array, and then iterates again\nfor each number to count its occurrences. As soon as a number is found to\nhave appeared more than any other can possibly have appeared, return it.

\n\n

Complexity Analysis

\n

\n
• \n

  Time complexity : $$O(n^2)$$ \n

  \n

  The brute force algorithm contains two nested for loops that each run\nfor $$n$$ iterations, adding up to quadratic time complexity.

  \n
\n
• \n

  Space complexity : $$O(1)$$ \n

  \n

  The brute force solution does not allocate additional space proportional\nto the input size.

  \n
\n

\n

---

\n

Approach #2 HashMap [Accepted]

\n

Intuition

\n

We know that the majority element occurs more than $$\\lfloor \\frac{n}{2} \\rfloor$$ \ntimes, and a HashMap allows us to count element occurrences efficiently.

\n

Algorithm

\n

We can use a HashMap that maps elements to counts in order to count\noccurrences in linear time by looping over nums. Then, we simply return the\nkey with maximum value.

\n\n

Complexity Analysis

\n

\n
• \n

  Time complexity : $$O(n)$$ \n

  \n

  We iterate over nums once and make a constant time HashMap insertion\non each iteration. Therefore, the algorithm runs in $$O(n)$$ time.

  \n
\n
• \n

  Space complexity : $$O(n)$$ \n

  \n

  At most, the HashMap can contain $$n - \\lfloor \\frac{n}{2} \\rfloor$$ \nassociations, so it occupies $$O(n)$$ space. This is because an arbitrary\narray of length $$n$$ can contain $$n$$ distinct values, but nums is\nguaranteed to contain a majority element, which will occupy (at minimum)\n $$\\lfloor \\frac{n}{2} \\rfloor + 1$$ array indices. Therefore,\n $$n - (\\lfloor \\frac{n}{2} \\rfloor + 1)$$ indices can be occupied by\ndistinct, non-majority elements (plus 1 for the majority element itself),\nleaving us with (at most) $$n - \\lfloor \\frac{n}{2} \\rfloor$$ distinct\nelements.

  \n
\n

\n

---

\n

Approach #3 Sorting [Accepted]

\n

Intuition

\n

If the elements are sorted in monotonically increasing (or decreasing) order,\nthe majority element can be found at index\n $$\\lfloor \\frac{n}{2} \\rfloor$$ (and $$\\lfloor \\frac{n}{2} \\rfloor + 1$$ ,\nincidentally, if $$n$$ is even).

\n

Algorithm

\n

For this algorithm, we simply do exactly what is described: sort nums, and\nreturn the element in question. To see why this will always return the\nmajority element (given that the array has one), consider the figure below\n(the top example is for an odd-length array and the bottom is for an\neven-length array):

\n

\n

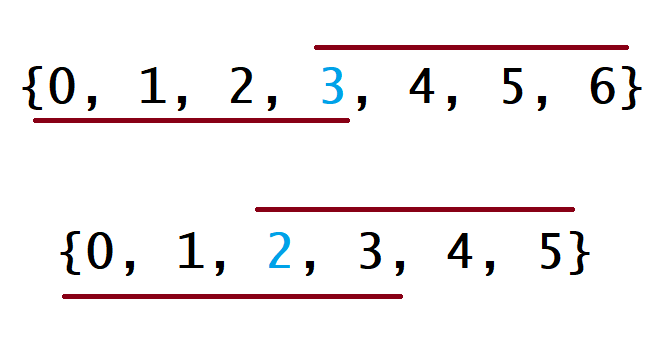
For each example, the line below the array denotes the range of indices that\nare covered by a majority element that happens to be the array minimum. As\nyou might expect, the line above the array is similar, but for the case where\nthe majority element is also the array maximum. In all other cases, this line\nwill lie somewhere between these two, but notice that even in these two most\nextreme cases, they overlap at index $$\\lfloor \\frac{n}{2} \\rfloor$$ for both\neven- and odd-length arrays. Therefore, no matter what value the majority\nelement has in relation to the rest of the array, returning the value at\n $$\\lfloor \\frac{n}{2} \\rfloor$$ will never be wrong.

\n\n

Complexity Analysis

\n

\n
• \n

  Time complexity : $$O(nlgn)$$ \n

  \n

  Sorting the array costs $$O(nlgn)$$ time in Python and Java, so it\ndominates the overall runtime.

  \n
\n
• \n

  Space complexity : $$O(1)$$ or ( $$O(n)$$ \n

  \n

  We sorted nums in place here - if that is not allowed, then we must\nspend linear additional space on a copy of nums and sort the copy\ninstead.

  \n
\n

\n

---

\n

Approach #4 Randomization [Accepted?]

\n

Intuition

\n

Because more than $$\\lfloor \\frac{n}{2} \\rfloor$$ array indices are occupied\nby the majority element, a random array index is likely to contain the\nmajority element.

\n

Algorithm

\n

Because a given index is likely to have the majority element, we can just\nselect a random index, check whether its value is the majority element,\nreturn if it is, and repeat if it is not. The algorithm is verifiably correct\nbecause we ensure that the randomly chosen value is the majority element\nbefore ever returning.

\n\n

Complexity Analysis

\n

\n
• \n

  Time complexity : $$O(\\infty)$$ \n

  \n

  It is technically possible for this algorithm to run indefinitely (if we\nnever manage to randomly select the majority element), so the worst\npossible runtime is unbounded. However, the expected runtime is far\nbetter - linear, in fact. For ease of analysis, convince yourself that\nbecause the majority element is guaranteed to occupy more than half of\nthe array, the expected number of iterations will be less than it would\nbe if the element we sought occupied exactly half of the array.\nTherefore, we can calculate the expected number of iterations for this\nmodified version of the problem and assert that our version is easier.

  \n

  \n $$\n\\begin{aligned}\n EV(iters_{prob}) &\\leq EV(iters_{mod}) \\\\\n &= \\lim_{n\\to\\infty} \\sum_{i=1}^{n} i \\cdot \\frac{1}{2^i} \\\\\n &= 2\n\\end{aligned}\n$$ \n

  \n

  Because the series converges, the expected number of iterations for the\nmodified problem is constant. Based on an expected-constant number of\niterations in which we perform linear work, the expected runtime is\nlinear for the modifed problem. Therefore, the expected runtime for our\nproblem is also linear, as the runtime of the modifed problem serves as\nan upper bound for it.

  \n
\n
• \n

  Space complexity : $$O(1)$$ \n

  \n

  Much like the brute force solution, the randomized approach runs with\nconstant additional space.

  \n
\n

\n

---

\n

Approach #5 Divide and Conquer [Accepted]

\n

Intuition

\n

If we know the majority element in the left and right halves of an array, we\ncan determine which is the global majority element in linear time.

\n

Algorithm

\n

Here, we apply a classical divide & conquer approach that recurses on the\nleft and right halves of an array until an answer can be trivially achieved\nfor a length-1 array. Note that because actually passing copies of subarrays\ncosts time and space, we instead pass lo and hi indices that describe the\nrelevant slice of the overall array. In this case, the majority element for a\nlength-1 slice is trivially its only element, so the recursion stops there.\nIf the current slice is longer than length-1, we must combine the answers for\nthe slice\'s left and right halves. If they agree on the majority element,\nthen the majority element for the overall slice is obviously the same¹. If\nthey disagree, only one of them can be "right", so we need to count the\noccurrences of the left and right majority elements to determine which\nsubslice\'s answer is globally correct. The overall answer for the array is\nthus the majority element between indices 0 and $$n$$ .

\n\n

Complexity Analysis

\n

\n
• \n

  Time complexity : $$O(nlgn)$$ \n

  \n

  Each recursive call to majority_element_rec performs two recursive\ncalls on subslices of size $$\\frac{n}{2}$$ and two linear scans of length\n $$n$$ . Therefore, the time complexity of the divide & conquer approach\ncan be represented by the following recurrence relation:

  \n

  \n $$\n T(n) = 2T(\\frac{n}{2}) + 2n\n$$ \n

  \n

  By the master theorem,\nthe recurrence satisfies case 2, so the complexity can be analyzed as such:

  \n

  \n $$\n\\begin{aligned}\n T(n) &= \\Theta(n^{log_{b}a}\\log n) \\\\\n &= \\Theta(n^{log_{2}2}\\log n) \\\\\n &= \\Theta(n \\log n) \\\\\n\\end{aligned}\n$$ \n

  \n
\n
• \n

  Space complexity : $$O(lgn)$$ \n

  \n

  Although the divide & conquer does not explicitly allocate any additional\nmemory, it uses a non-constant amount of additional memory in stack\nframes due to recursion. Because the algorithm "cuts" the array in half\nat each level of recursion, it follows that there can only be $$O(lgn)$$ \n"cuts" before the base case of 1 is reached. It follows from this fact\nthat the resulting recursion tree is balanced, and therefore all paths\nfrom the root to a leaf are of length $$O(lgn)$$ . Because the recursion\ntree is traversed in a depth-first manner, the space complexity is\ntherefore equivalent to the length of the longest path, which is, of\ncourse, $$O(lgn)$$ .

  \n
\n

\n

---

\n

Approach #6 Boyer-Moore Voting Algorithm [Accepted]

\n

Intuition

\n

If we had some way of counting instances of the majority element as $$+1$$ \nand instances of any other element as $$-1$$ , summing them would make it\nobvious that the majority element is indeed the majority element.

\n

Algorithm

\n

Essentially, what Boyer-Moore does is look for a suffix $$suf$$ of nums\nwhere $$suf[0]$$ is the majority element in that suffix. To do this, we\nmaintain a count, which is incremented whenever we see an instance of our\ncurrent candidate for majority element and decremented whenever we see\nanything else. Whenever count equals 0, we effectively forget about\neverything in nums up to the current index and consider the current number\nas the candidate for majority element. It is not immediately obvious why we can\nget away with forgetting prefixes of nums - consider the following\nexamples (pipes are inserted to separate runs of nonzero count).

\n

[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]

\n

Here, the 7 at index 0 is selected to be the first candidate for majority\nelement. count will eventually reach 0 after index 5 is processed, so the\n5 at index 6 will be the next candidate. In this case, 7 is the true\nmajority element, so by disregarding this prefix, we are ignoring an equal\nnumber of majority and minority elements - therefore, 7 will still be the\nmajority element in the suffix formed by throwing away the first prefix.

\n

[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 5, 5, 5, 5]

\n

Now, the majority element is 5 (we changed the last run of the array from\n7s to 5s), but our first candidate is still 7. In this case, our\ncandidate is not the true majority element, but we still cannot discard more\nmajority elements than minority elements (this would imply that count could\nreach -1 before we reassign candidate, which is obviously false).

\n

Therefore, given that it is impossible (in both cases) to discard more\nmajority elements than minority elements, we are safe in discarding the\nprefix and attempting to recursively solve the majority element problem for the\nsuffix. Eventually, a suffix will be found for which count does not hit\n0, and the majority element of that suffix will necessarily be the same as\nthe majority element of the overall array.

\n\n

Complexity Analysis

\n

\n
• \n

  Time complexity : $$O(n)$$ \n

  \n

  Boyer-Moore performs constant work exactly $$n$$ times, so the algorithm\nruns in linear time.

  \n
\n
• \n

  Space complexity : $$O(1)$$ \n

  \n

  Boyer-Moore allocates only constant additional memory.

  \n
\n

\n

---

\n

Footnotes

\n

---

\n

Analysis written by: @emptyset

\n

Approaches and time complexities itemized by @ts and @1337c0d3r

\n\n