All leaked interview problems are collected from Internet.
56. Merge Intervals
Given a collection of intervals, merge all overlapping intervals.
For example,
Given [1,3],[2,6],[8,10],[15,18],
return [1,6],[8,10],[15,18].
b'
Approach #1 Connected Components [Time Limited Exceeded]
\nIntuition
\nIf we draw a graph (with intervals as nodes) that contains undirected edges\nbetween all pairs of intervals that overlap, then all intervals in each\nconnected component of the graph can be merged into a single interval.
\nAlgorithm
\nWith the above intuition in mind, we can represent the graph as an adjacency\nlist, inserting directed edges in both directions to simulate undirected\nedges. Then, to determine which connected component each node is it, we\nperform graph traversals from arbitrary unvisited nodes until all nodes have\nbeen visited. To do this efficiently, we store visited nodes in a Set,\nallowing for constant time containment checks and insertion. Finally, we\nconsider each connected component, merging all of its intervals by\nconstructing a new Interval with start equal to the minimum start among\nthem and end equal to the maximum end.
This algorithm is correct simply because it is basically the brute force\nsolution. We compare every interval to every other interval, so we know\nexactly which intervals overlap. The reason for the connected component\nsearch is that two intervals may not directly overlap, but might overlap\nindirectly via a third interval. See the example below to see this more\nclearly.
\n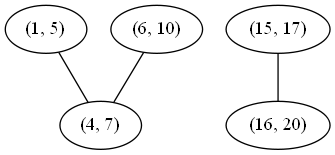
Although (1, 5) and (6, 10) do not directly overlap, either would overlap\nwith the other if first merged with (4, 7). There are two connected\ncomponents, so if we merge their nodes, we expect to get the following two\nmerged intervals:
\n(1, 10), (15, 20)
\n\nComplexity Analysis
\n- \n
- \n
Time complexity : \n
\nBuilding the graph costs \ntime, as in the worst case all intervals are mutually overlapping.\nTraversing the graph has the same cost (although it might appear higher\nat first) because our
\nvisitedset guarantees that each node will be\nvisited exactly once. Finally, because each node is part of exactly one\ncomponent, the merge step costs time. This all adds up as\nfollows:\n\n
\n \n - \n
Space complexity : \n
\nAs previously mentioned, in the worst case, all intervals are mutually\noverlapping, so there will be an edge for every pair of intervals.\nTherefore, the memory footprint is quadratic in the input size.
\n \n
\n
Approach #2 Sorting [Accepted]
\nIntuition
\nIf we sort the intervals by their start value, then each set of intervals\nthat can be merged will appear as a contiguous "run" in the sorted list.
Algorithm
\nFirst, we sort the list as described. Then, we insert the first interval into\nour merged list and continue considering each interval in turn as follows:\nIf the current interval begins after the previous interval ends, then they\ndo not overlap and we can append the current interval to merged. Otherwise,\nthey do overlap, and we merge them by updating the end of the previous\ninterval if it is less than the end of the current interval.
A simple proof by contradiction shows that this algorithm always produces the\ncorrect answer. First, suppose that the algorithm at some point fails to\nmerge two intervals that should be merged. This would imply that there exists\nsome triple of indices , , and in a list of intervals\n such that and (, ) can be\nmerged, but neither (, ) nor (, )\ncan be merged. From this scenario follow several inequalities:
\n\n\n
\nWe can chain these inequalities (along with the following inequality, implied\nby the well-formedness of the intervals: ) to\ndemonstrate a contradiction:
\n\n\n
\nTherefore, all mergeable intervals must occur in a contiguous run of the\nsorted list.
\n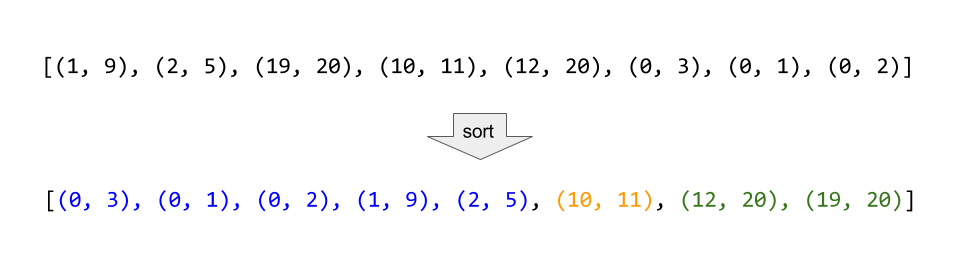
Consider the example above, where the intervals are sorted, and then all\nmergeable intervals form contiguous blocks.
\n\nComplexity Analysis
\n- \n
- \n
Time complexity : \n
\nOther than the
\nsortinvocation, we do a simple linear scan of the list,\nso the runtime is dominated by the complexity of sorting. \n - \n
Space complexity : (or )
\nIf we can sort
\nintervalsin place, we do not need more than constant\nadditional space. Otherwise, we must allocate linear space to store a\ncopy ofintervalsand sort that. \n
\n
Analysis and solutions written by: @emptyset
\n