Solution

Approach #1 (Brute Force) [Time Limit Exceeded]

Algorithm

Each time sumRegion is called, we use a double for loop to sum all elements from $$(row1, col1) \\rightarrow (row2, col2)$$ .

private int[][] data;\n\npublic NumMatrix(int[][] matrix) {\n    data = matrix;\n}\n\npublic int sumRegion(int row1, int col1, int row2, int col2) {\n    int sum = 0;\n    for (int r = row1; r <= row2; r++) {\n        for (int c = col1; c <= col2; c++) {\n            sum += data[r][c];\n        }\n    }\n    return sum;\n}\n

Complexity analysis

\n
• \n

  Time complexity : $$O(mn)$$ time per query.\nAssume that $$m$$ and $$n$$ represents the number of rows and columns respectively, each sumRegion query can go through at most $$m \\times n$$ elements.

  \n
\n
• \n

  Space complexity : $$O(1)$$ . Note that data is a reference to matrix and is not a copy of it.

  \n
\n

Approach #2 (Caching) [Memory Limit Exceeded]

Intuition

Since sumRegion could be called many times, we definitely need to do some pre-processing.

Algorithm

We could trade in extra space for speed by pre-calculating all possible rectangular region sum and store them in a hash table. Each sumRegion query now takes only constant time complexity.

Complexity analysis

\n
• \n

  Time complexity : $$O(1)$$ time per query, $$O(m^2n^2)$$ time pre-computation.\nEach sumRegion query takes $$O(1)$$ time as the hash table lookup\'s time complexity is constant. The pre-computation will take $$O(m^2n^2)$$ time as there are a total of $$m^2 \\times n^2$$ possibilities need to be cached.

  \n
\n
• \n

  Space complexity : $$O(m^2n^2)$$ .\nSince there are $$mn$$ different possibilities for both top left and bottom right points of the rectangular region, the extra space required is $$O(m^2n^2)$$ .

  \n
\n

Approach #3 (Caching Rows) [Accepted]

Intuition

Remember from the 1D version where we used a cumulative sum array? Could we apply that directly to solve this 2D version?

Algorithm

Try to see the 2D matrix as $$m$$ rows of 1D arrays. To find the region sum, we just accumulate the sum in the region row by row.

private int[][] dp;\n\npublic NumMatrix(int[][] matrix) {\n    if (matrix.length == 0 || matrix[0].length == 0) return;\n    dp = new int[matrix.length][matrix[0].length + 1];\n    for (int r = 0; r < matrix.length; r++) {\n        for (int c = 0; c < matrix[0].length; c++) {\n            dp[r][c + 1] = dp[r][c] + matrix[r][c];\n        }\n    }\n}\n\npublic int sumRegion(int row1, int col1, int row2, int col2) {\n    int sum = 0;\n    for (int row = row1; row <= row2; row++) {\n        sum += dp[row][col2 + 1] - dp[row][col1];\n    }\n    return sum;\n}\n

Complexity analysis

\n
• \n

  Time complexity : $$O(m)$$ time per query, $$O(mn)$$ time pre-computation.\nThe pre-computation in the constructor takes $$O(mn)$$ time. The sumRegion query takes $$O(m)$$ time.

  \n
\n
• \n

  Space complexity : $$O(mn)$$ .\nThe algorithm uses $$O(mn)$$ space to store the cumulative sum of all rows.

  \n
\n

Approach #4 (Caching Smarter) [Accepted]

Algorithm

We used a cumulative sum array in the 1D version. We notice that the cumulative sum is computed with respect to the origin at index 0. Extending this analogy to the 2D case, we could pre-compute a cumulative region sum with respect to the origin at $$(0, 0)$$ .

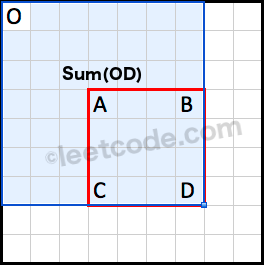
\nSum(OD) is the cumulative region sum with respect to the origin at (0, 0).

How do we derive $$Sum(ABCD)$$ using the pre-computed cumulative region sum?

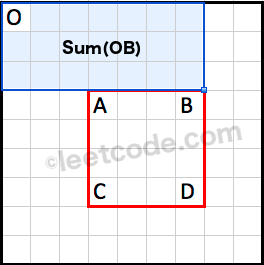
\nSum(OB) is the cumulative region sum on top of the rectangle.

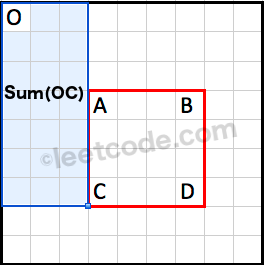
\nSum(OC) is the cumulative region sum to the left of the rectangle.

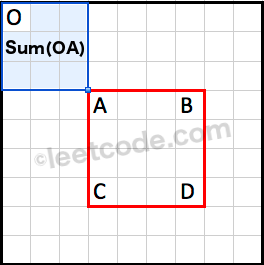
\nSum(OA) is the cumulative region sum to the top left corner of the rectangle.

Note that the region $$Sum(OA)$$ is covered twice by both $$Sum(OB)$$ and $$Sum(OC)$$ . We could use the principle of inclusion-exclusion to calculate $$Sum(ABCD)$$ as following:

\n $$\nSum(ABCD) = Sum(OD) - Sum(OB) - Sum(OC) + Sum(OA)\n$$ \n

private int[][] dp;\n\npublic NumMatrix(int[][] matrix) {\n    if (matrix.length == 0 || matrix[0].length == 0) return;\n    dp = new int[matrix.length + 1][matrix[0].length + 1];\n    for (int r = 0; r < matrix.length; r++) {\n        for (int c = 0; c < matrix[0].length; c++) {\n            dp[r + 1][c + 1] = dp[r + 1][c] + dp[r][c + 1] + matrix[r][c] - dp[r][c];\n        }\n    }\n}\n\npublic int sumRegion(int row1, int col1, int row2, int col2) {\n    return dp[row2 + 1][col2 + 1] - dp[row1][col2 + 1] - dp[row2 + 1][col1] + dp[row1][col1];\n}\n

Complexity analysis

\n
• \n

  Time complexity : $$O(1)$$ time per query, $$O(mn)$$ time pre-computation.\nThe pre-computation in the constructor takes $$O(mn)$$ time. Each sumRegion query takes $$O(1)$$ time.

  \n
\n
• \n

  Space complexity : $$O(mn)$$ .\nThe algorithm uses $$O(mn)$$ space to store the cumulative region sum.

  \n
\n